Using expression trees to build up loops - Gauss Summation

I tested out Expression trees today in more depth and played around with Gauss summation. The Gauss summation is a well-known theorem in Calculus. It states that for a plain arithmetic sequence of numbers with a distance of 1 (i.e. 1,2,3,4,5,6...) from 1..n the sum of these numbers are equal to the formula : Sum(n) = (n*(n+1)) / 2 Johan Karl Friendrich Gauss is renowned to have come up with this as a very young student when a school teacher asked the class to sum the numbers from 1 to 100 and give him the answer. Gauss almost instantly replied '5050', which was also the correct answer. This may or may not have been the case. The formula itself can anyways be theorized by summing the largest and
smallest number and then approaching the middle of the sequence. You can add 1 and 100 to get 101, 2 and 99 to get 101 and so on. The sum is always 101 (n+1) and there are a hundred such 'pairs' (n). But we want to only sum the numbers once, so we divide by 2 => we have the Gauss summation formula ! Let's look at how to do such a summation using Expression trees in C#. But I have only created a loop algorithm here, we calculate the same answer but we instead use expression trees. In demonstrates how
we can get started with expression trees in C# using loops (it is while loop which is created here) and parameter expressions and other components, such as 'labels' used in 'gotos'. This is actually needed in
expression trees to get the looping and breaking to work. The 'SumRange' method looks like this :

public static Expression SumRange(ParameterExpression value)
{
    LabelTarget label = Expression.Label(typeof(int));

    ParameterExpression result = Expression.Variable(typeof(int), "result");
    var initializeResult = Expression.Assign(result, Expression.Constant(0));

    var innerLogicBlock = Expression.Block(
        Expression.Assign(result,
            Expression.Add(result, value)),
        Expression.PostDecrementAssign(value)
    );

    BlockExpression body = Expression.Block(
       new[] { result },
       initializeResult,
       Expression.Loop(
           Expression.IfThenElse(
            Expression.GreaterThanOrEqual(value, Expression.Constant(1)),
            innerLogicBlock,
            Expression.Break(label, result)
            ),
            label
         )
    );
    return body;
}

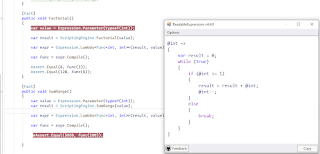
We pass in a parameter expression. We then declare a 'label' which is used in a 'goto' execution flow when we want to break out of our loop, created by Expression.Loop. The initializeResult is listed here inside Expression block as we want to assign the result variable to the initial value (the expression constant '0'). We then have an 'outer logic' where we have a If-Then-Else condition where we check if value is greater than or equal to 1 and then
we perform the 'inner logicl block' assigned earlier, where we assign result to itself and the value variable passed in as a parameterexpression to this method. Note, we will do some type checking via Expression.Lambda which call this SumRange method explained further below. Note the use of 'PostDecrementAssign' expression which decrements the 'value' and ensures we can exit out of the loop. It can be of course hard to follow along such expression trees without some tooling. I use the ReadableExpressions:Visualizer plugin for VS 2022 here : https://marketplace.visualstudio.com/items?itemName=vs-publisher-1232914.ReadableExpressionsVisualizers You can use it to preview expressions as shown in the below screen shot :

And our unit test passes with expected result.

 

        [Fact]
        public void SumRange()
        {
            var value = Expression.Parameter(typeof(int));
            var result = ScriptingEngine.SumRange(value);
            var expr = Expression.Lambda<Func<int, int>>(result, value);
            var func = expr.Compile(); 
             Assert.Equal(5050, func(100)); 
        }

 

As you can see, even for a simple method, we need to type a lot of code to build up an expression tree. There are helper libraries such as AgileObjects.ReadableExpressions and System.Linq.Dynamic.Core which
can help out a lot when using expression trees. Add these to your package references (.csproj) for example :

  <ItemGroup>
    <PackageReference Include="AgileObjects.ReadableExpressions" Version="3.3.0" />
    <PackageReference Include="System.Linq.Dynamic.Core" Version="1.2.18" />
  </ItemGroup>

The first package of these got a handy method ToReadableString and the last one got a handy helper class called DynamicExpressionParser, which in tandem can create pretty complex expression trees. When will you use such logic ? Most often when wanting to build up custom logic query filters. You should not allow end users to arbitrarily build up all kinds of query filters, but may offer them a set of user controls to build and combine query filters so they can retrieve data via rather complex rules. The code libs mentioned here is supported in .NET Framework 3.5 or later (and .NET Standard 1.0), so most target frameworks are supported then.

Get properties of a given type in C#

This article shows how we can find all properties with a given property type. The provided code also can find private properties or look for nullable of the property type. E.g. find all DateTime properties and also include all properties which are Nullable of DateTime, Nullable. An extension method for this looks like the following (put the method into a static class as it is an extension method) :

  

  
          /// <summary>
        /// Retrieves a list of properties (property info) with given type <paramref name="propertyType"/> in a nested object
        /// </summary>
        /// <param name="rootObject"></param>
        /// <param name="propertyType"></param>
        /// <param name="includePrivateProperties">If set to true, includes private properties</param>
        /// <param name="includeNullableVariant">If set to true, return also propertie which are the nullable variant of the <paramref name="propertyType"/>.</param>
        /// <returns>A list of properties with given <paramref name="propertyType"/>, possibly including also non-nullable variant of the type and both public and private properties set with the parameters <paramref name="includePrivateProperties"/> and <paramref name="includeNullableVariant"/></returns>
        public static IEnumerable<PropertyInfo> GetPropertiesOfType(this object rootObject, Type propertyType,
            bool includePrivateProperties = false, bool includeNullableVariant = false)
        {
            if (rootObject == null)
            {
                yield return null;
            }
            var bindingFlagsFilter = !includePrivateProperties ? BindingFlags.Public | BindingFlags.Instance : BindingFlags.Public | BindingFlags.NonPublic | BindingFlags.Instance;
            var propertiesOfType = rootObject.GetType().GetProperties(bindingFlagsFilter)
                .Where(p => p.PropertyType == propertyType || (includeNullableVariant && propertyType == Nullable.GetUnderlyingType(p.PropertyType)))
                .ToList();
            foreach (var prop in propertiesOfType)
            {
                yield return prop;
            }
            var nestableProperties = rootObject.GetType().GetProperties(bindingFlagsFilter)
              .Where(p => p.PropertyType.IsClass && p.PropertyType != typeof(string))
              .ToList(); //ignoring properties of type strings as they are not nested, though a class
            foreach (var prop in nestableProperties)
            {
                if (prop.GetIndexParameters().Length > 0)
                {
                    continue; //skip indexer properties 
                }
                var rootObjectLevel = prop.GetValue(rootObject, null);
                if (rootObjectLevel == null)
                {
                    continue;
                }
                foreach (var propertyAtLevel in GetPropertiesOfType(rootObjectLevel, propertyType, includePrivateProperties, includeNullableVariant))
                {
                    yield return propertyAtLevel;
                }
            }
        }

We find the properties matching the property type and then recursively fetch such properties at nested levels too if the property is a class and therefore can contain sub properties. We end up with all the properties of a given type. As we see, we adjust the binding flags to include private properties too or not. And we use the Nullable.GetUnderlyingType method to match the underlying type in case we want to look for DateTime and DateTime? properties. This method is fairly fast, in the order of a few milliseconds (1-5 when I tested for an ordinary two level nested object.) But we are using reflection here and the method could be faster if we made use of some other techniques, perhaps with
IL 'magic'. I have not found a way to do this yet though.. Here is another utility method (extension method) for finding 'property paths'. This is handly if you want to craft an SQL select statement for example as we need the fully qualified path perhaps if our tooling creates fields in the database similar to POCO object
and the nested object is similar to table structure. Maybe your nested properties are mapped to SomeInnerTable1_SomeField1 and so on. Anyways, it is handly to have 'property paths' to the properties to get a fast overview of where the properties are located in the nested structure of your (possibly complex) object.

         /// <summary>
        /// This method looks for properties of given type in a nested object (e.g. a form data contract) 
        /// </summary>
        /// <param name="rootObject"></param>
        /// <param name="propertyType"></param>
        /// <returns></returns>
        private IEnumerable<string> GetPropertyPathsForType(object rootObject, Type propertyType, string prefixAtLevel = "")
        {
            if (rootObject == null)
            {
                yield return string.Empty;
            }
            var propertiesOfType = rootObject.GetType().GetProperties(BindingFlags.Public | BindingFlags.Instance)
                .Where(p => p.PropertyType == propertyType)
                .ToList();

            foreach (var prop in propertiesOfType)
            {
                if (string.IsNullOrWhiteSpace(prefixAtLevel))
                {
                    yield return prop.Name; //root properties have no prefix 
                }
                else
                {
                    yield return prefixAtLevel.TrimStart('.') + "." + prop.Name;
                }
            }

            var nestableProperties = rootObject.GetType().GetProperties(BindingFlags.Public | BindingFlags.Instance)
              .Where(p => p.PropertyType.IsClass && p.PropertyType != typeof(string))
              .ToList(); //ignoring properties of type strings as they are not nested, though a class

            foreach (var prop in nestableProperties)
            {
                if (prop.GetIndexParameters().Length > 0)
                {
                    continue; //skip indexer properties - this is identified as required 
                }
                var rootObjectLevel = prop.GetValue(rootObject, null);
                if (rootObjectLevel == null)
                {
                    continue;
                }
                foreach (var propertyAtLevel in GetPropertyPathsForType(rootObjectLevel, propertyType, prefixAtLevel + "." + prop.Name))
                {
                    yield return propertyAtLevel.TrimStart('.').TrimEnd('.');
                }
            }
        }

The code above could use the first method more to support including public and private properties, but I leave it out 'as an exercise to the reader' as text books often states. So this code is very handy if you for example at work need to find 'all the datetime properties in a domain object' and similar cases. Maybe you want to deny all datetimes have a future datetime in case it is a report for a patient treatment report being performed yesterday and so on, and for
that particular model, there will be no future date time values.